What is Tower of Hanoi problem write an algorithm to solve Tower of Hanoi problem?

Introduction to Recursion :

• Here, I am going to talk about recursion. Basically, what is recursion a recursive method or a recursive procedure is where the solution to a problem depends on solutions to smaller instances of the same problem.
• So, we break the task into smaller subtasks. And the approach can be applied to many types of problems. And because of this recursion is one of the central ideas of computer science. So very important that we have to define a so-called base case to avoid infinity loops and also important to know that we can solve a given problem either with iteration or with recursion.

Recursion Implementation

• So, if we have a recursion implementation, we can transform it into an iterative implementation and vice versa. So, if we have an iterative implementation, we can transform it into a recursive one. For example, we can solve lots of data structure related problems such as binary search tree insert, link lists removal and so on. So, these kinds of operations can be implemented with the help of recursive method calls.
• But of course, if we prefer iteration these kinds of problems can be solved with the help of iteration as well. So, recursion and iteration are interchangeable. So, for example, we want to add first N integers. Usually, we use a simple for loop, but we can solve it with the help of recursion.

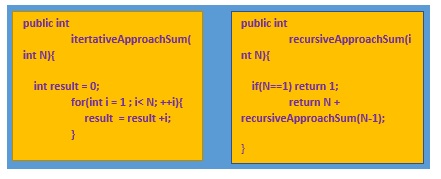
• So, the iterative approach is quite straightforward. We initialize the result variable. We iterate through all the numbers and we keep adding them. So, this is how we sum up all the integers and we return the given result.
• Then we have the recursive approach. We define the base case. This is what we have been discussing that we have to define the base case to avoid infinity loops. If we had not defined this based case, the algorithm would run forever so it would be an infinite loop. So, as you can see that we have a given problem and we can solve the subproblem – 1 with the same approach. So, that's why we can use recursion.

What's the difference between Head and tail recursion?

In the case of at the end of the method, if the recursive call occurs, then it is called the tail recursion. So, the tail recursion is just similar to a given loop and a method executes all the statements before jumping into the next recursive call.

Tail Recursion:

• So, for example, this is tail recursion.

Public void tail(int N) { if(N==1) return; system.out.printIn(N); tail(N-1); }

Of course, we have to define the base case no matter whether it is a tail recursion or a head recursion. But for tail recursion, the recursive call is at the end of the method. And here we just printout the given number but we can do whatever operation we want with this given parameter. So, that's all about tail recursion.

Head Recursion:

In the case of the beginning of the method if the recursive call occurs, then it is called the head recursion and in case of Head recursion, before jumping into the next recursive call, the method saves the state. So, what's very important that as you can see here?

Public void head (int N) { if(N==1) return; head(N-1); system.out.printIn(N); }

• We call this method recursively and then we do something with that given the variable this is the recursion and we have to save the given state we have to save the given variables and so on. So that's all about tail recursion when we call the method recursively at the end and head recursion is when we call the method recursively at the beginning of the method.
• It's extremely important that we have to use the base case no matter what. So, as you can see if (N==1), we return for the tail recursion and head recursion as well. So, this is what we have been discussing that we have to store the pending calls, we have to store the arguments and we have to use a stack abstract data type for this purpose.
• So, we have the track during recursion who calls the given method and what arguments are to be handed over. And we have to track the pending cause as well. So, we just need a single stack abstract data type. And what's very important that the operating system does everything for us. So that's why you could pose the question that why don't we use a stack abstract data type here to track the pending calls and argument?
• Because the operating system is going to use the stack memory for this purpose. So, this important information are to be pushed onto the stack and values are popped from the stack. So, we use the stack to store this information.
• So, let's see a concrete example we would like to calculate the sum of the first N integers. For example, we call this method as recursionSum method() with the integer 4. What's going to happen.

Public int recursionSum(int N) { if(N ==1) return 1; return N + recursionSum(N-1); }

• We have the base case but if the N!=1, then we call this method recursively on a smaller integer as you can see in above screenshot. But what's very important that we don't know the value of this. So that's why it's going to be pushed onto the stack memory. So, we know that the N is equal to 4 because we call that method with the integer 4. But we do not know the value of this recursionSum. So that's why this recursion method call is going to be pushed onto the stack with the value 3.
• We call this recursionSum with integer 3. It is not the base case. Again, we push a given method call onto the stack. We know that the “N” value in this case 3 plus recursionSum minus one. That's why its argument is going to be 2. So, we call this method recursively with the integer 2 and as 2 is not equal to 1 so, this is not the base case. So, again we push on to the stack the two-plus we call this method recursively with the integer 2 minus 1 which is 1. And in this case, this is the base case we call this recursionSum() with the integer one and if N==1, and this is the base case here and we return 1.

• So, essentially, we all know that now the worth is one and thence, we tend to are ready to come back as you'll be able to see, we tend to come back one. As a result of now, we all know that the recursionSum(1) wherever the argument is 1==1. (2+1 -> 3+ recusrionSumMethod(2)).
• That’s why it’s about to be 2 and one and it’s about to come to its position. It’s about to be 3+2+1 and since we all know the precise price goes to be came to the current position. (3+2+1) -> four + recusrionSumMethod(3))
• So finally, we all know that if we decide this recursionSum method () with whole number four, then it's about to come back four and 3 and 2 and one that is adequate to ten. Therefore, final output is going to be four +3+2+1=10

This is all concerning what is happening within the background. We tend to decision these strategies recursively:

When we use recursionSum (int N) method: When we use recursionSum(int N) method: recursionSum(4); recursionSum(3); recursionSum(2); recursionSum(1); return 1; return 2+1; return 3+2+1; return 4+3+2+1;

• The above Method calls are to be pushed onto the stack till we tend to hit the bottom case. Till the bottom case we tend to be ready to double back essentially and replace these method calls with the precise values wished a pair of and one, 3+2+1 and eventually 4+3+2+1. So, these technique calls, and therefore the values keep on the stack. And what concerning examination algorithmic implementation with reiterative implementation.

Why Recursion is slower?

• Recursion is a minimum of doubly slower as a result of 1st we have a tendency to unfold recursive calls (updating them onto stack). This can be what I am talking that we tend to keep pushing the strategy goes onto the stack till we tend to come across the bottom case, so we tend to traverse the stack and retrieve all the algorithmic calls.
• So that is why as you'll be able to see 1st, we have a tendency to push the things onto the stack then we have a tendency to keep returning items from the stack. And that is why your algorithmic approach i.e. the recursive approach is a minimum of doubly slower thanks to these operations.

Differences between the iterative approach and the recursive approach :

• We have been discussing the contrasts between the iterative methodology and the recursive methodology. Along these lines, we should take a solid model. I will make another Java web development project. What’s more, I will make the iterative methodology just like the recursive methodology. Along these lines, most importantly we will have a class calculation and the bundle name will be anything. What's more, in this class, we will have the iterative methodology of how to entirety the primary whole numbers.
• So, I will have a public strategy and we get a given number and we are going to a portion of those numbers. Thus, for instance when the "n" is equivalent to 3 then we are going to a portion of the 3 + 2 + 1. When the "n" is equivalent to 10, we will amount of 10 + 9 + 8 + … +1. Thus, this is the thing that we are after. Most importantly, we need to make an outcome variable and it is equivalent to zero toward the start.
• And then we need to repeat. Along these lines, whole number is equivalent to 1 it is not exactly, or equivalent "n" and we simply need to state that the outcome is equivalent result+ I. Thus, this is the very basic iteration.

Public class RecursiveAlgo { public int sumIterativeApproach(int num) { int sum = 0; for(int i:i<=num: ++i) { sum = sum+i; } } }

• This is the thing that we have been talking about in that specific segment that the iterative methodology typically contains a for circle or some time circle and obviously toward the end we need to get back with the outcome.
• So, we should see if it's turned out great. I will make an application that Java to have the option to pass or calculations so we will have the primary strategy. We need to start up the calculation like underneath. Also, we simply need to printout the calculation and I might want to utilize the iterative methodology and I might want to aggregate/summation of the initial three whole numbers. Alright, how about we run it and it should yield three in addition to two in addition to 1 which is equivalent to 6...

Public class AppTest { Public static void main (String[] args) { RecursiveAlgo algo = new RecursiveAlgo(); System.out.printIn(algo.sumIterativeApproach(3)); } }

• So, this working fine with any n value. And this is what we have been discussing that if we will implement an iterative approach, then we would be able to transform it into a recursive one. And if we will have a recursive approach, then definitely we would be able to transform it into an iterative version. So basically, everything a problem can be solved either with iteration or with recursion.
• So, shouldn't something be said about the recursive calculation? Above all else, we need to characterize the base case and afterward a public technique. Furthermore, that technique will take input boundary given a whole number and if that a whole number is equivalent to 1. This is the base case we bring one back.
• And in any case, if we will return the n in addition to we call this some recursive capacity on a sub undertaking or a subproblem. We need to pass n-1 since we need to add for instance 5. Also, after we have thought about five, we need to consider the whole number decremented by 1. Along these lines, Four, Three, and 2 than one, etc. until we hit the base case. Alright, so we should see if it's turned out great.

Public int recursiveSum (int n) { if(n==1) return 1; return n + recursiveSum(n-1) }

• I clarified the iterative methodology, and this is the recursive methodology for a similar issue. In this way, I might want to settle some recursive with fire and we ought to get 15 once more. Alright, it will turn out great.

Public class AppTest { public static void main(String[] args) { RecursiveAlgo algo=new RecursiveAlgo(); System.out.printIn(algo.recursiveSum(5)); } }

What about so, we have resolved. We have been examining it in a hypothetical area, yet we have executed it also that every issue can be addressed with cycle and the iterative methodology comprises of a for circle or some time circle and we can settle it with the assistance of recursion

Towers of Hanoi:

So, what are these Towers of Hanoi?

• It comprises three rods and several plates/disks of various sizes which can slide onto any rod. The riddle begins with the circles in a slick stack in a rising request of size on one rod/pole the littlest at the top consequently making the alleged tapered shape. The base number of moves needed to take care of the Towers of Hanoi issue is Two to the power of and short 1(2n - 1). Along these lines, this is the number of moves we need to make. That is the reason the running time's multifaceted nature will be remarkable. For example, O(2n).
• It is nothing but an algorithm that is quite slow. Along these lines, we have a few principles. Just one disk/circle/plate can be moved at a given time. Each move comprises taking the upper plate from one of the stacks and putting it on top of another stack. Thus, we can't control the center plate. This must be moved on the off chance that it is the highest plate on the stack.
• And what's more significant that no plate might be set on top of for a more modest plate/circle. By this way there's a legend concerning the Towers of Hanoi are that Indian clerics were to move a pinnacle comprising 64 plates starting with one piece of the sanctuary then onto the next with similar rulers. In this way, these were the standards.
• So, one plate at a given time and a bigger plate may never be set up on a more modest one. Also, it is said when the ministers/priests total their work, the world will reach its endpoint. Furthermore, the inquiry is the number of moves is there. This is the thing that we have been talking about here to get a force off "n" where the "n" indicates the number of plates. For this situation, there are 64 circles or 64 plates. So that is the reason there are two to the intensity of 64 short one (264 - 1) moves. This is the number of moves the clerics need to make.
• So, here what is about the real issue? We have three rods/bars. This is the starting rod. This is the middle of the rod or the so-called auxiliary rod. And we have the final road order and the end road. There are the plates at the beginning. And as you can see, we are not able to put a greater plate on top of the smaller ones. So that's why we have the greatest one than the second greatest one and the smallest one.

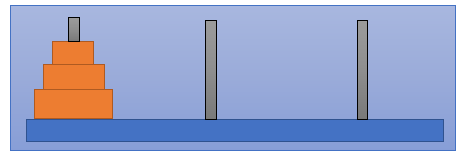
• And the aim is that we have to make sure that these plates will be transferred to the last road and making sure that we met the towers of Hanoi principles. So basically, we can move one plate at a given time and no disk may be placed on top of a smaller disk. So, we can solve it for a very little problem like this that we have to shift the disk to the last rod. Then we have to shift the disk to the auxiliary road. Then we have to shift the last rod disk back to auxiliary one.
• And this is a very important step that we have managed to put all the plates from the largest one onto the auxiliary rod. And that's why we are able to move the greatest one on to its final position.

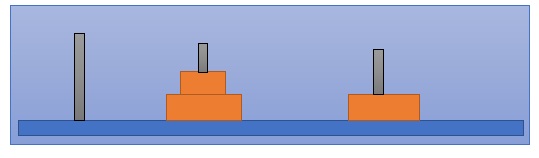
• And then we have to move this auxiliary pile of plates into the last rod basically with the help of the first rod. So, we can put it there. We can shift it there and we can put it onto the top of them.

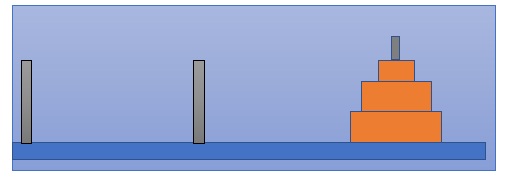
• So, as you can see this is how we can solve the Tower of Hanoi problem for just 3 Plates/Disks. But what's very important that we can consider the subproblems. So, this is the starting position. We have the three plates on the starting rod and there will be a situation like this. So, there will be always a situation where we have to shift (n-1) plates to the auxiliary rod. Why n-1 plates, because the last one is still in its original position. So, we have managed to shift n-1 disks to the auxiliary rod.
• And if we just have to do the largest one to the last rod. And what's very important that this is going to be the same problem not for the n plates but for n-1 plates. Because this one(last rod plate) is considered to be in its final position as it is the greatest plate, we can place any of the other remaining plates on the top of the greatest one because this is the greatest one. We are not going to violate the tower of Hanoi principles.
• We can consider the last rod disk to be in its final position. We don't have to bother about it anymore and we just have to consider the leftover n-1 one plates. And we just have to put it there in the first rod. So, if we have four plates, the algorithm is the same. We have to make sure that we shift n-1 one plate to the auxiliary rod. We have to shift the last one to its final position and it's very important to see that in this case, the auxiliary rod will be the first one. We can start over the algorithm, but in this case, an auxiliary rod is the starting rod.

The last one is the final rod where we have to shift all of the plates. But again, the first rod is going to be the auxiliary rod wherewith which we can able to solve this problem.

Towers of Hanoi Implementation :

• How to solve Towers of Hanoi with the help of recursion. So, I'm going to define the public void solveHanoi() method. So, the method we are going to get the number of disks and then we get characters.
• We will have the source, the middle rod and then we have the destination as an input parameter. Of course, we have to define the base case. So, if the n value is zero that means n is here the disk value so, this is the integer representation of the disk so we can use something like this is equal to zero. We are going to deal with three plates/disks. Please find below the code snippet :

Public void solveHanoi(int n, char source, char middle, char dest) { if(n==0) { solveHanoi(n-1,source,dest,middle); System.out.printIn(“plate”+n+”from”+source+”to”+dest); // moving n-1 plates from mid rod to dest rod with the help of source rod solveHanoi(n-1, middle, source, dest); } }

• The smallest one will have an index zero. The middle will have the index one. And the largest plate or largest disk has the integer representation 2. So, whenever the disk is close to zero, it means that this is the base case and it has something to do with the smallest plate. So, we return, and we print out that plate and we append the disk and from and we append the source and then we append the two. And of course, we have to append the destination in the logs.
• In this case, the disk equals zero. This is the base case. This is when they move the smallest plate. And otherwise, what do we have to do? We have to call this method recursively with n-1. In this case, we have source, middle, and destination. So we have the three rods accordingly. And here we move the n-1 plates to the middle rod to be able to move the largest one to the destination or the last rod.
• So, this is why we have to make sure that the source is going to be the source. So, the first rod then with the half of the destination, we would like to end up with the middle rod. We would like to place the n-1 plates from the first rod. So, the source to the middle rod with the help of the destination or the last rod, and after that, we can move the given plate. So, we move the large plate to the destination. By the way, we must call this method recursively. So, this is not always the largest plate.
• In the beginning, we have the three plates at the first rod, then, and there's going to be a situation like when n-1 plates are in the middle of the rod and we have to shift the largest one to the final position and then we have to place n-1 plate’s recursively on the top of the largest plate.
• So, first of all, we move n-1 plates to the middle of the rod, then we move the actual largest one to the destination. And after that, we move this n-1 plate from the middle of the rod to the destination.
• So, we have done something like the above code snippet. We moved n-1 plates from the middle to the destination with the help of the first rod. So, what do we have to do? We move this n-1 from the middle with the help of the source to the destination or last rod. So, from the middle of the rod with the help of the source, the first road to the destination road.
• For calling our method solveHanoi(), we can instantiate the class and then we just have to call the solveHanoi(2, ‘X’, ‘Y’, ‘Z’); method. And in this case, the number of disks i.e. n value is equal to three. But note that indices start with zero. So, in this case, we have to define it too, because there is values zero one-two. If we define three, then there's going to be four values. So, this is why we have to define just 2 and we have to define the name of the rods. The source road is a letter “X”, then we have the middle rod “Y” and the destination rod is “Z”. So, if we save and run the application, then as you can see, it is going to work just fine.

FAQs:

Subject: Algorithmic Problems in Java and Towers of Hanoi Problem Implementation

• What do you mean by Algorithmic problems in Java?
• Difference between Recursive and Iterative approach?
• How to implement Towers of Hanoi Problem?
• What are the basic differences between Head Recursion and Tail Recursion?
• Why recursion is always slower?