What is the Bellman equation & How it is derived for Solving Reinforcement Learning?

Introduction to Probability Trees:

One useful way to think about value functions is probability trees. Although these are somewhat simplistic as you'll see very soon as a simple example consider a biased coin with probability of heads equals zero point six (0.6). The idea behind the probability tree is the root node is going to represent where I am now. All the child nodes represent the states I could possibly go next. Each branch of the tree has a way which tells us the probability of going through that state. From this graph:

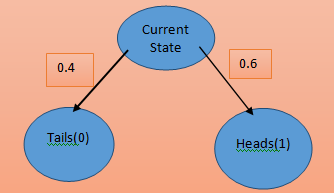
• I can see that I have a 40 percent chance of going to the left and getting zero reward and I have a 60 percent chance of going right and getting a reward of 1 if heads equals 1 and tails you go zero. It's obvious that my expected reward will be one time zero point six plus zero times the point four which is equal to zero point six(0.6). In other words, my expected reward is the weighted sum of all the possible rewards where those weights are given by the branches of the tree.
  
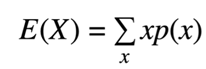
• Note that the supplies to a tree that can have any number of children. The rule remains the same. The expected value is the weighted sum of each of the child node values weighted by the respective probabilities. Of course, this is just the definition of the expected value for a discrete random variable. If X is our random variable, then the expected value of x is just the sum over all possible values of x of X times P of X.
• Of course, we can extend this concept even further. Let's look at a game of tic tac toe. Previously we looked at a very simple tree where there was only a root node and then direct descendants of the root node with tic tac toe. We have to consider the fact that the game isn't over after just a single move in tic tac toe.

Example of Game Tree:

• A game is played by doing an entire sequence of moves and thus we have an entire sequence of states. Each leaf node in the tree represents a possible state that we might end up in. This game tree represents all the different trajectories we might take from where we are in the tree at the current moment. Luckily the same thought process still applies. We want to do is calculate the expected some future rewards which ends up being some kind of weighted sum of the values of the descendants.
• The nice thing about trees is that they should remind us of recursion. Remember that a tree is a recursive data structure. We can pick any child node in our tree and the sub tree starting at that child node is also itself a tree. Recursion: G1 = R2 + R3 + … + RT G2 = R3 + … + RT G1 = G2 + R2
• Let's look carefully at the equation above for the return we say that it's the sum of future rewards. G1 will be equal to R2 plus our 3 all the way up to our big T. But what if we are at the next time step and we want to know what G2 is. Well using the definition G2 is just our three plus for all the way up to our big T.
• Notice how g 2 is actually embedded into G 1. In other words, we can substitute G2 into the expression for G1. G1 is just R2 plus G2 in general we can say that g of T is equal to R of T plus 1 plus g of T plus 1.

I would like you to prove to yourself that this applies to discounted returns as well.

With Discounting:

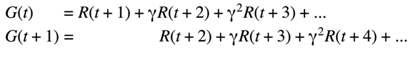
• G of time t is equal to R of T plus 1 plus gamma times already plus two plus gamma squared times already plus three and so on. Yes T plus 1 is equal to Rof T plus two plus gamma times are T plus three plus gamma square at times are T plus four and so on. Therefore, G of time t Ziegler R T plus 1 plus gamma times G of T plus 1.
• We can summarize this by saying the return is recursive but let's remember that we are not just interested in the return but rather the expected return having an expected value makes this a bit more complicated. Still this shouldn't stop us from trying. We haven't expected value. Now let's try to expand our expression for the expected value using the relevant probabilities. To take our first step in deriving the Belmont equation.
  
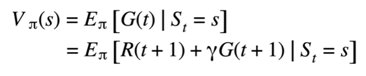
• Let's remember that the return is recursive so I can replace Gof time t with our R of time t plus 1 plus gamma times Gof time T plus 1. The next step is the trickiest step out of this entire derivation to understand this step. We first have to understand the law of total expectation in general.
  
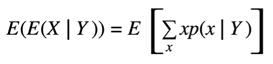
• This says that the expected value of the expected value of x given a Y is just the expected value of x. That is if we take the expected value of a conditional expectation, it doesn't matter what we are conditioning on that thing disappears. To show you why this is true you only have to expand the expression by the definition of the expected value.
• We start by expanding the inner expected value which is a conditional expectation. The random variable here is X. So, we sum over x. The next step is to expand to the outer expected value since the inner expected value has already summed over x. The random variable now is Y. Thus, our outer sum should be over y. Since this is an expectation over the random variable Y, the appropriate probability distribution is p of Y.
  
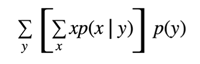
• In the next step. We remove the extraneous brackets since they don't affect the order of operation. In the next step we recognize that P of X given y times P of Y.
  
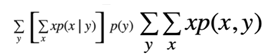
• It's just the joint probability p of x and y in the next step. We move the sum over y inside past all the X's that's allowed. Since nothing to the left of Y depends on Y. Of course, this is just marginalization. The sum over p of x and y over y just gives us P of X. Now we have the sum over x of X times P of X which as we know is the expectation of x.
  

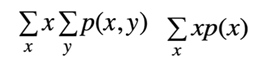
How to use Law of Total Expectation?

• So how can we use the law of total expectation to help us derive the rest of the Belmont equation? Well it might help to first recognize that the expectation is a linear operation. So, if we see a plus sign inside an expectation, we can split up the expectation. That expectation of a sum is the sum of expectations.
  
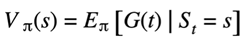
• We can also bring constants outside like gamma. The important part of this is the second term. The term with the return that g of T plus 1. This is like our X in the law of total expectation as you know we can replace g of T plus 1 with any conditional expectation.
• But obviously we want to replace it with something that makes sense. So how about the next state as prime at timest plus 1 of course this is nothing but the definition of the value function at the state as prime.
  
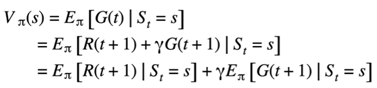
• And so, we can simply replace it with a symbol V of s prime and put both terms back together under the same expected value.

What is The Bellman Equation: The Main Piece of Reinforce Learning

Reinforcement Learning:

Reinforcement Learning, basically a part of Machine Learning, is about making a reasonable move to discover the most ideal performance or path it should take in a particular circumstance. It also assists you to increase some part of the aggregate reward. Hiring professional team to robotize your business processes will gives you start to finish machine learning development services depends on the most recent algorithms. Reinforcement algorithms are praised as the eventual fate of Machine Learning as these removes the expense of collecting and cleansing the data.

Here, it is the Bellman equation for the value function: The centerpiece of reinforcement learning.

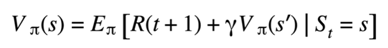
• Although it seems simple it has one key characteristic. This is that the computation of the value function is recursive. Calculating the value function at the current state “s” depends only on the possible next states as prime. There is no need to say traverse a possibly infinite number of future trajectories to estimate the expected value. In other words, you don't need to search an entire probability tree.
• What this equation says is that in order to calculate V of s you only need to look at one step ahead. The value at as prime why is this remarkable. It means that our agent can plan without actually having to look very far in the future. Even if our goal is 1 million steps ahead, we can plan those entire 1 million steps simply by solving this equation that only looks at the next step.

What are the distributions that you need to Sum Over?

• It's important to recognize what probability distributions in the Belmont equation we are actually summing over. As I have explained you earlier the value of a state is dependent on both the state but also the policy we are following. That's the probability distribution pie. And we even write this explicitly as a subscript.
  
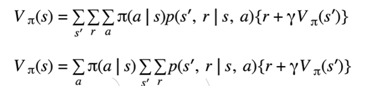
• What is not is clear is that, the value also depends on the environment dynamics. Of course, now that I say this it's pretty obvious. Obviously, the expected sum of future rewards would depend on the environment itself. Recall that in an MVP there are two entities the agent and the environment and they both have their own respective probability distributions.
• The agent is represented by pi of a given s and the environment is represented by P of as prime and “r” given S&A. Therefore, if we expand out the expression for the Belmont equation, both of these probabilities should appear. Note that in this above expression snapshot, the random variables we need to sum over are as prime. The next state are the reward and “a” the action.
• It might not be clear exactly why expanding the Belmont equation like this is useful but later you'll do some exercises to help you see how to use it. One way to simplify this equation a bit is to recognize that the policy distribution pie does not depend on s prime or R so it can be brought outside those sums. Now we only have one outermost sum over and the sums over s primary NA can be brought further inside.

Alternative Forms of Bellman Equation:

• I want to mention that there are some alternative forms of a Bell equation that you will see out in this blog. You recall I had mentioned earlier that sometimes the reward is not considered to be stochastic just the next state. In other words, the reward is dependent on these three values.
  
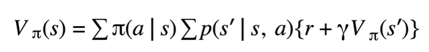
• In that case we can simplify Bowman's equation the environment dynamics are now represented by P of s prime given s.
• Another notation which is a little more verbose makes the dependence of the reward more explicit. Essentially, it's subscript the reward with a triple. The current state “s”, the action “a” and the next state as Prime.
  
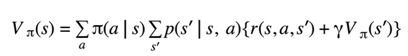
• One alternative notation which is kind of odd in my opinion is to use subscript and superscript instead of explicitly stating: “what's the random variable in what's being conditioned on”. Of course, this is not ideal since we can't see what the meaning of any of these distributions is. It also confuses the policy as a joint distribution rather than a conditional distribution. I will never use this, but I want you to know that it exists.

Idea of Probability Trees:

• Finally, I want to bring this back to the idea of probability trees. The thing with probability trees is that we can only go in one direction, but we know that this is limited even in a game like chess. If the players just keep moving their pieces back and forth although you probably wouldn't want to do so your game will just go back and forth between states that were already visited.
• Another example of this is if you are modeling the weather. Suppose we have three states sunny rainy and cloudy.
  
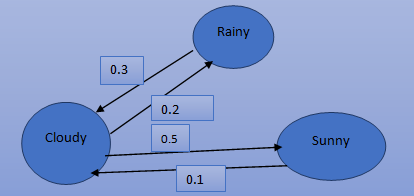
• Obviously, we can go from any state to any other state from one day to the next including the option of staying in the same state. For example, it's sunny two days in a row as you already know previously, calculating expected values in a tree is easy you just some over the child knows. But what if you have a generic graph that has loops. Now there is no notion of child because you can have two nodes that are pointing at each other.

What do you mean by Linear Equations and its usefulness?

• My claim is that solving the Belmont equation becomes nothing but a system of linear equations to remind you of what these looks like although you should already know this. Consider a set of two equations:
x + y = 7 and another is 2x-y = 2
• X plus Y equals 7 and 2 x minus y equals 2. This is two equations and two unknowns and so usually from these we can solve for x and y. Well the Bellman equation is the same.

Detailed Explanation of Linear Equations Usefulness

Suppose we have two states as one and as two we can go from S1 to S2 or vice versa and we can stay in the same state remember that for now we will consider that environment dynamics and policy distribution to be given.

• If we look carefully at our Bellman equation what do we see. First let's consider pie since this is given, it's just a constant. It's just a number. Now let's consider P of s prime are given s in a since this is also given it is also a constant. Now let's consider ah well this is known since P of s prime are given us “s” and “a” is known.
  
  • Here Vπ(S′) and Vπ(S) -> Variable
  • Here, s and a are assumed to be known
• We are just summing over all possible values of R. How about V of as prime? Well this can only take on it two possible values i.e. V of s1 or V of s 2. Therefore, it's easy to see that the Belmont equation boils down to two equations. The first equation is v of s 1 equals B1 plus c11 at times V of s1 one plus C12V of times s2.
• The second equation is v of s2 equals B2 plus C 21 at times V of s2 plus C 22 times V as 2. Please find below the two equations:
  
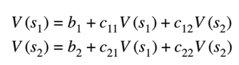
• Here are the bees and Caesar constants and thus the Belmont equation is really nothing but a set of linear equations. So, what's wrong with solving the Bellman equation using a system of linear equations? Well the problem is that the number of variables is the number of possible states.
• What would we do for games like chess or go which have tens of the 50 or 10 to the 170 states (10 50 or 10 170). In cases like these solving systems of linear equations is not possible. Unfortunately, problems like these are also the kinds of problems that we care about. We also haven't yet discussed problems with a state space are infinite. Thus, in our Bellman advance blog you can go through for learning how to solve the Bellman equation also how to solve in a way that is also scalable.

Last Words

Recalling about twenty years prior, the software development market in those days had a totally dissimilar situation contrasted with what it is presently. Software development is difficult and maintaining the apps through different advancement levels is very much hard. A custom software application development company will help to grow your business with cutting-edge development tools and achieves the utmost potential of building the software at their fingertips.

The significant changes that Software Company discovers now are the freedom to build up the applications. They have the ability to establish the particular and tailor-make apps for your business platform. Custom Software will turn into a spine to your business movement and the Software Development organizations will back you with their responsive, powerful and high-performing services.